Introduction

In this part of the paper, I explain how to integrate the polynomial, from First Principles. You should have read the previous parts of the series before reaching here, as this is the continuation.

Integration is area under the curve.
Consider the following diagram:

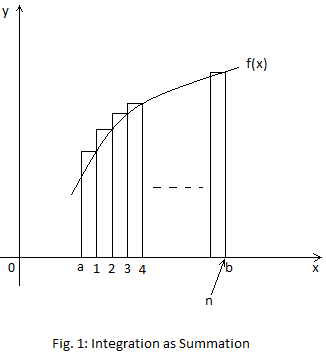
y = f(x)

You might have seen the following:

This statement is not perfect. It should actually be:

where f(x_n) is a particular height from the curve to the x-axis.

My Discovery

The widths of the vertical strips are equal.

As 𝛿x turns to 0, the number of strips increases.

n is the total number of strips.

As 𝛿x → 0, n → ∞

The series and the formula for its summation, for all the heights of the strips from a to b, is obtained. If you do not know the formula for the series, develop one, and that may take time. Summing is done for the heights, from 1 to n.

The summation expression above in the statement, is replaced with the summation formula.

As n → ∞ the right-hand-side of the statement becomes the definite integral; and that concludes the scheme.

Let total area be represented by A. So, my statement for the Integration from First Principles is:

In the following analysis, Pascal's Triangle has been used in the binomial expansions.

Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be S_n.

Here,

y = C

i.e.

f(x) = C

S_n = (C₀ + C + C + C + - - - + C_n-1)𝛿x

      = (nC) 𝛿x

But $\mathrm{\delta <!--GREEK\; SMALL\; LETTER\; DELTA-->}x=\frac{b-a}{n}$

⸫ S_n = $nC\frac{b-a}{n}$

The n_s cancel:

=> S_n = C(b - a)

=> S_n = Cb - Ca

As n → ∞,

A = Cb - Ca ………………….the definite integral

If a is 0 and b is x,

I = Cx ………………………..the indefinite integral

For the general term, r^m, you need my general formula pattern for the power series, which is:

Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be S_n.

Here,

y = x⁰

i.e.

f(x) = x⁰

But $\mathrm{\delta <!--GREEK\; SMALL\; LETTER\; DELTA-->}x=\frac{b-a}{n}$ $$\therefore <!--THEREFORE-->S_n=\left[n\right]<!--INVISIBLE\; TIMES-->\frac{b-a}{n}$$

The n_s cancel:

=> S_n = b - a

=> S_n = b - a

As n → ∞,

A = b - a ………………….the definite integral

If a is 0 and b is x,

I = x ………………………..the indefinite integral

For the general term, r^m, you need my general formula pattern for the power series, which is:

Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be S_n.

Here,

y = x¹

i.e.

f(x) = x¹

Rearranging gives:

Adjusting the multipliers and multiplicands, give

My formulas for the power series of index 0 and 1 are:

and

$\mathrm{\delta <!--GREEK\; SMALL\; LETTER\; DELTA-->}x=\frac{b-a}{n}$

Substituting for δx and the summation series with the formulas, give

The n_s and the n²_s cancel, giving:

As n → ∞, the term with denominator 2n, turns to 0. So

Notice that there is only one term in b² in the evaluation. Also, the combined terms in a and b subtract out, while the terms in a² sign-sum to 1/2 of a².

If a is 0 and b is x,

For the general term, r^m, you need my general formula pattern for the power series, which is:

Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be S_n.

Here,

y = x²

i.e.

f(x) = x²

Rearranging gives:

My formulas for the power series of index 0, 1 and 2 are:

and

and

$\mathrm{\delta <!--GREEK\; SMALL\; LETTER\; DELTA-->}x=\frac{b-a}{n}$

Substituting for δx and the summation series with the formulas, give

The n_s, n²_s and n³_s cancel, giving:

As n → ∞, the terms with denominators in n, turn to 0. So

Notice that only the first term of the resulting expressions-per-line have been taken (did not turn to 0).

Notice that there is only one term in b³ in the evaluation. Also, the combined terms in a and b subtract out, while the terms in a³ sign-sum to 1/3 of a³.

If a is 0 and b is x,

For the general term, r^m, you need my general formula pattern for the power series, which is:

Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be S_n.

Here,

y = x³

i.e.

f(x) = x³

Rearranging gives:

My formulas for the power series of index 0, 1, 2 and 3 are:

and

and

and

$\mathrm{\delta <!--GREEK\; SMALL\; LETTER\; DELTA-->}x=\frac{b-a}{n}$

Substituting for δx and the summation series with the formulas, give

The n_s, n²_s, n³_s and n⁴_s cancel, giving:

As n → ∞, the terms with denominators in n, turn to 0. So

Notice that only the first term of the resulting expressions-per-line have been taken (did not turn to 0).

Notice that there is only one term in b⁴ in the evaluation. Also, the combined terms in a and b subtract out, while the terms in a⁴ sign-sum to 1/4 of a⁴.

If a is 0 and b is x,

Here,

y = x^m

i.e.

f(x) = x^m

Each of the above evaluations, makes use of the general formula pattern,

for the different power series, which differ by their indexes.

In each evaluation, n^m+1 cancels off. The other terms in n, turn to zero as n turns to infinity. The terms in b and a subtract out. The terms in a, sign-sum to 1/(m+1) of a^(m+1). There is only one term for b^(m+1), which is (1/(m+1))b^(m+1). So,

If a is 0 and b is x,

where C is a constant.

Here,

y = Cx^m

i.e.

f(x) = Cx^m

If a is 0 and b is x,

Integration is area under the curve. A polynomial is a summation of polynomial terms. So integration of a polynomial is the summation of the integrals of each term. Some of the individual areas, may have negative values.

This is the end of this part of the series. Continue in the next part.

Chrys