Introduction

Integration is area under the curve.
Consider the following diagram:

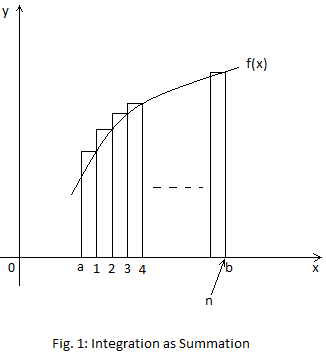
y = f(x)

You might have seen the following:

This statement is not perfect. It should actually be:

where f(x_n) is a particular height from the curve to the x-axis.

My Discovery

The widths of the vertical strips are equal.

As 𝛿x turns to 0, the number of strips increases.

n is the total number of strips.

As 𝛿x → 0, n → ∞

The series and the formula for its summation, for all the heights of the strips from a to b, is obtained. If you do not know the formula for the series, develop one, and that may take time. Summing is done for the heights, from 1 to n.

The summation expression above in the statement, is replaced with the summation formula.

As n → ∞ the right-hand-side of the statement becomes the definite integral; and that concludes the scheme.

Let total area be represented by A. So, my statement for the Integration from First Principles is:

Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be S_n.

Here,

y = C

i.e.

f(x) = C

S_n = (C₀ + C + C + C + - - - + C_n-1)𝛿x

      = (nC) 𝛿x

But $\mathrm{\delta <!--GREEK\; SMALL\; LETTER\; DELTA-->}x=\frac{b-a}{n}$

⸫ S_n = $nC\frac{b-a}{n}$

The n_s cancel:

=> S_n = C(b - a)

=> S_n = Cb - Ca

As n → ∞,

A = Cb - Ca ………………….the definite integral

If a is 0 and b is x,

I = Cx ………………………..the indefinite integral

The Document

In the next part of the series, I explain the algorithm and formula pattern for the power series that I have developed (invented). The rest of the document explains, integration from first principles, of the polynomial term, the reciprocal of the polynonial term, trigonometric functions, etc. Many of the function types, integrated in the high school and in British Further Mathematics subject, by reversal of differentiation, are integrated here from first principles.

Chrys