Task score : 100% -  Correctness : 100% ; Performance : 100%

Detected time complexity : O(N)

Lesson 10 at app.codility.com/programmers

The solution and its explanation are given below.

Category of Article : Technology | Computers and Software | Algorithm 

Problem

A non-empty array A consisting of N integers is given.

A peak is an array element which is larger than its neighbours. More precisely, it is an index P such that 0 < P < N - 1 and A[P − 1] < A[P] > A[P + 1]. 

For example, the following array A:

    A[0] = 1

    A[1] = 5

    A[2] = 3

    A[3] = 4

    A[4] = 3

    A[5] = 4

    A[6] = 1

    A[7] = 2

    A[8] = 3

    A[9] = 4

    A[10] = 6

    A[11] = 2 

has exactly four peaks: elements 1, 3, 5 and 10.

You are going on a trip to a range of mountains whose relative heights are represented by array A, as shown in the figure below. You have to choose how many flags you should take with you. The goal is to set the maximum number of flags on the peaks, according to certain rules. 

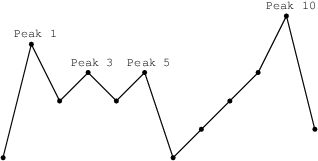
Flags can only be set on peaks. What's more, if you take K flags, then the distance between any two flags should be greater than or equal to K. The distance between indices P and Q is the absolute value |P − Q|. 

For example, given the mountain range represented by array A, above, with N = 12, if you take:

        two flags, you can set them on peaks 1 and 5;

        three flags, you can set them on peaks 1, 5 and 10;

        four flags, you can set only three flags, on peaks 1, 5 and 10. 

You can therefore set a maximum of three flags in this case.

Write a function:

    function solution(A); 

that, given a non-empty array A of N integers, returns the maximum number of flags that can be set on the peaks of the array.

For example, the following array A: 

    A[0] = 1

    A[1] = 5

    A[2] = 3

    A[3] = 4

    A[4] = 3

    A[5] = 4

    A[6] = 1

    A[7] = 2

    A[8] = 3

    A[9] = 4

    A[10] = 6

    A[11] = 2

the function should return 3, as explained above. 

Write an efficient algorithm for the following assumptions:

        N is an integer within the range [1..400,000];

        each element of array A is an integer within the range [0..1,000,000,000]. 

Note

The maximum number of peaks (not flags) is N/2 (integer division). This occurs, if at every distance of 2, there is a peak.

If N is less than 3, then there can be no peak. If N is 3, there is one peak, and 1 has to be returned as the maximum number of flags. 

A quotation from the problem (question) is, "What's more, if you take K flags, then the distance between any two flags should be greater than or equal to K." This means that if there are two peaks altogether, the maximum number of flags is 2, assuming that K is at least 2. Note that the minimum possible distance between peaks is 2.

As K increases tentatively, the number of flags increases. This continuous until a point is reached, where, as K increases, the number of flags decreases. So there is a maximum number of flags within the range of K. It is this maximum that is required. 

Illustration

For example, given the mountain range represented by array A, above, with N = 12, if you take:

- two flags, you can set them on peaks 1 and 3 or other combinations of at least distance two (maximum no. of flags is 2);

- three flags, you can set them on peaks 1, 5 and 10 (maximum no. of flags being 3);

- four flags, you can set only three flags, on peaks 1, 5 and 10 (no. of flags above maximum);

- five flags, you can set only two flags, on peaks 1 and 10 or 5 and 10 (no. of flags above maximum);

- six flags, you can set only two flags, on peaks 1, and 10 (no. of flags above maximum).

Note that the last two operations (even last three) are wasted operations, and the solution should stop (for-loop should break) and not execute wasted operations (not increase the time complexity).

Strategy

An array for the indexes of all the peaks is first obtained (in N time). This array is called, peakIndexes in the code below.

There is then a for-loop that iterates from K=2 to a maximum of K=N/2. The break is within this loop just after the maximum is reached. There is a nested for-loop in this outer four-loop, that counts the number of flags.

The counter counts the number of flags that are set (number of flags set is not necessarily the number of flags taken along). This is done in the nested for-loop. Within the nested for-loop, the counter should not go above K, which is the number of flags carried by you to the mountains. Consider the case of K=2 above. After two flags have been set at indexes 1 and 3, another flag can be set at index 5, making the count 3. Yet another can be set at index 10, making the count 4. So within the nested for-loop, the counter should not go above K, which is the number of flags carried by you to the mountains.

The maximum count for all the possible different values of K, is what is returned.

In the overall algorithm, once the distance (indexes) between two peaks is greater than or equal to K, a flag is set.

Smart Solution

A solution() function is in the following program (read the code and comments):

<script type='text/javascript'>
    "use strict";

function solution(A) {
    let N = A.length;
    if (N<3) return 0;    //there can be no peak
    
    const peakIndexes = [];
    for(let i=1;i<N-1;i++){
        if ((A[i-1]<A[i])&&(A[i+1]<A[i]))
            peakIndexes.push(i);
    }
    
    let noPeaks=peakIndexes.length;
    if (noPeaks<3) return noPeaks;  //also to prevent out-of-bounds error (Segmentation fault (core dumped))
    
    let max=2;    //from minimum of two peaks
    for(let K=2; K <= N/2; K++){    
        let counter = 1;
        let P = peakIndexes[0];
        for(let i=1; i<peakIndexes.length && counter < K; i++){  //counter can become K inside this nested loop
            if (peakIndexes[i] - P >= K){
                counter++; 
                P = peakIndexes[i];
            }
        }
 
        if (counter > max)
            max = counter;
        else if (counter < max)    //just past maximum
            break;
    }
    
    return max;
}

const V1 = [1, 5, 3, 4, 3, 4, 1, 2, 3, 4, 6, 2];
let ret1 = solution(V1);
document.write(ret1 + '<br>');

const V2 = [3, 2, 1];    //can cause out-of-bounds error
let ret2 = solution(V2);
document.write(ret2 + '<br>');

</script>

The output is:

    3

    0

At app.codility.com/programmers the scoring and detected time complexity for this solution() is:

    Task score : 100% -  Correctness : 100% ; Performance : 100%

    Detected time complexity : O(N)

app.codility.com/programmers did not include the number of operations to obtain the indexes of all the peaks for the array, peakIndexes. Including this will make the time complexity O(N+N). In the for-loops (with one nested), not all possible operations occurred.

When the total number of peaks is two, there cannot be more than two flags set, so 2 has to be returned as the maximum number of flags set. This is also why the variable, max, starts at 2.

Algorithm and the Given Data

Now, the algorithm for the given data is explained as follows:

One of the assumptions in the problem is: "N is an integer within the range [1..400,000];" . When N is 1, there can be no peak, so 0 is returned. When the number of peaks is less than 3, one is returned if there is one peak, or 2 is returned if there are two peaks.

After that, the minimum number of peaks that can be returned is 2 and the 2 is assigned to the variable, max. Thereafter, the for-loop begins from K=2 and will end at K=N/2, which is the maximum number of peaks the data can have. The counter for the maximum number of flags possible, for the value of K=2 is set to 1, and the index for the first peak (from the left of the mountains) for the same value of K=2 is assigned to the variable, P. In the nested for-loop, the counter is incremented up to 2 for K=2, for distances for at least K=2. For the given data, the value of the counter will end at 2, for peaks at indexes, 1 and 3. Before this iteration of the outer for-loop ends, the value 2 of the counter is compared to the presumed max value of 2. At this point, they are the same, and the outer for-loop does not break. The outer for-loop goes to the iteration of K=3.

The counter is reset to 1 and the index of the leftmost peak is assigned to P again. The nested for-loop then continue to increment the counter for each distance of at least 3 peaks. The counter will end at the value of 3 for the peak indexes of 1, 5 and 10. The value of K for the outer for-loop is at 3. Before this iteration of the outer for-loop ends, the value 3 of the counter is compared to the presumed max value, still at 2. At this point, the value of the counter is greater than the presumed max of 2 and the new max becomes 3. The outer for-loop goes to the iteration of K=4.

The counter is reset to 1 and the index of the leftmost peak is assigned to P again. The nested for-loop then continue to increment the counter for each distance of at least 4 peaks. The counter will end at the value of 3 for the peak indexes of 1, 5 and 10. The value of K for the outer for-loop is at 4. Before this iteration of the outer for-loop ends, the value 3 of the counter is compared to the presumed current max value of 3. At this point, the value of the counter is the same as the current presumed max of 3. If the value of K goes to 5, the counter will count from 1 to 2 after each distance of at least 5 peaks. 2 is less than 3. So the maximum value required is 3 and has been attained at K=3 and K=4. At this point, the outer for-loop breaks and ends, and the value of 3 is returned before the solution() function ends.

Comment

The knowledge of the lesson (Prime and Composite Numbers) has not really been used here. Only the idea of dividing a bigger integer by a smaller integer, has been used.

A quotation from the problem (question) is:

“For example, given the mountain range represented by array A, above, with N = 12, if you take:

        two flags, you can set them on peaks 1 and 5;”

When there are two flags, any two combinations of the four peaks is possible. The examiner intends to de-rail the candidate by indicating peak 1 and peak 5 as the only possible pair.